At the first Conference on Automated Machine Learning (AutoML), the work on Automatic termination for hyperparameter optimization won a best-paper award for a new way to decide when to stop Bayesian optimization, a widely used hyperparameter optimization method. In this blog post, we, i.e., the authors of the paper, intuitively explain the main aspects of this work.
The performance of machine learning models crucially depends on their hyperparameters, but setting them correctly is typically a tedious and expensive task. Hyperparameter optimization (HPO) requires iteratively retraining the model with different hyperparameter configurations in a search for a better one. This poses a question of the trade-off between the time use and the accuracy of the resulting model. The current work on Automatic termination for hyperparameter optimization suggests a new principled stopping criterion for this problem. At its core, it admits the discrepancy between the generalization error (i.e., true but unknown optimization objective) and its empirical estimator (i.e., objective optimized by HPO). That hints at the intuitive stopping criterion that is triggered once we are unlikely to improve the generalization error.
Hyperparameter optimization as black-box optimization
HPO can be seen as black-box optimization where we sequentially interact with a fixed unknown objective \(f(\gamma)\) and for a selected input \(\gamma_t\) observe its noise-perturbed evaluation \(y_t\). In HPO, the black-box function to be minimized is a population risk, i.e., performance of the model \(\mathcal{M}_\gamma\) trained on some data \(\mathcal{D}\) (e.g., via SGD) evaluated on the unseen data from the distribution \(P\). In the evaluation, we observe the noise-perturbed result with the stochasticity coming from the model training.

Bayesian optimization (BO) is a powerful framework for such black-box functions. In its core, for the function \(f\) with the optimizer \(\gamma^*\), BO searches for better predictive performance via (i) training a probabilistic model (e.g., Gaussian process (GP) or Bayesian neural network) on the evaluations and (ii) acquiring the most promising next hyperparameter candidate. This iterative search lasts until, for example, some user-defined budget. The goal is to minimize the distance between optimal \(\gamma^*\) and the best configuration \(\gamma_t^*\) found before the budget is used. This distance \(f(\gamma_t^*) – f(\gamma^*)\) quantifies the convergence of the HPO algorithm.
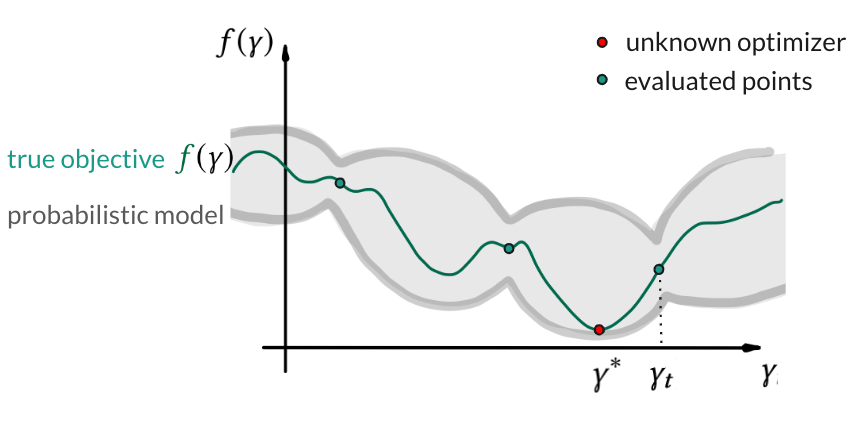
The discrepancy between the true objective and the computable HPO target
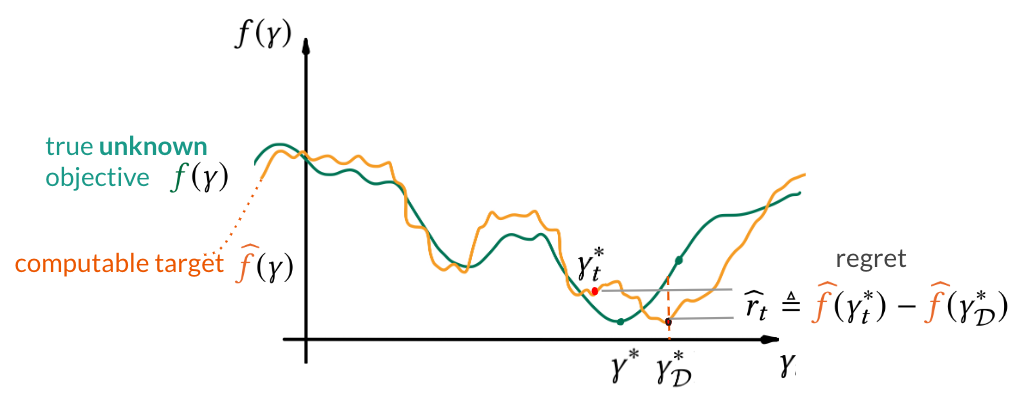
In the paper, we qualitatively address the question “whether \(f\) is actually the objective we optimize in practical BO”. The answer is no since the data distribution is unknown in practice. What we actually optimize (and evaluate) is the estimator of the population risk. That is, for some given data (divided into train-validation-test) we evaluate validation set-based value. As the result, the evaluation \(y_t\) inherits stochasticity not only due to the (1) stochasticity in model training; but also due to (2) data realization.
That highlights the discrepancy between what we would like to optimize and what we can optimize. As the result, optimizing the empirical estimator too strenuously may actually lead to sub-optimal solutions to the population risk.

Convergence criterion for hyperparameter optimization
Due to the discrepancy in the objectives, the quality of configurations is judged according to the empirical estimator \(\widehat f\) instead of the true objective \(f\). Namely, it is quantified by the regret \(\widehat r_t = \widehat f(\gamma_t^*) – \widehat f(\gamma_D^*)\) computed for the true optimizer \(\gamma: \hat{f} \to \widehat{f}\) and the best-found solution \(\gamma_t^*\) (see the figure below).
Our termination criterion is based on the observation that the evaluation of a particular hyperparameter configuration inherits the statistical error of the empirical estimator. By the statistical error, we mean, for example, its variance indicating how far, on average, the collection of evaluations is from the expected value. If the statistical error dominates the regret, further reduction of the regret may not improve notably the generalization error. However, neither the statistical error nor the true regret is known. In the paper, we show how to compute estimates of both quantities.
Building blocks of the termination criterion
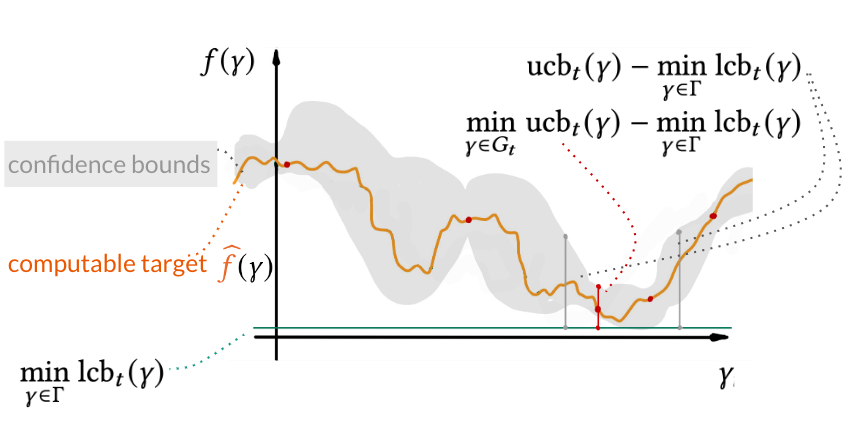
Bounding the regret
We derive the regret bounds from the probabilistic model used in Bayesian optimization. The key idea behind the bound is that as long as the model, namely the Gaussian process, is well-calibrated, the function: \(\hat f \to \widehat{f} \) lies in the interval with upper and lower confidence bounds (see \(\mathrm{ucb}\) and \(\mathrm{lcb}\) below). These are theoretically studied concentration inequalities valid under common assumptions used in BO and HPO (see the paper). Thus, the regret bound can be obtained via the distance between the upper and lower bounds on the function.
Bounding the statistical error
We show how one estimates the statistical error in the case of the prominent cross-validation-based estimator. The characteristics of this estimator, namely bias and variance, are well theoretically studied, which equips us with the ways to estimate them.
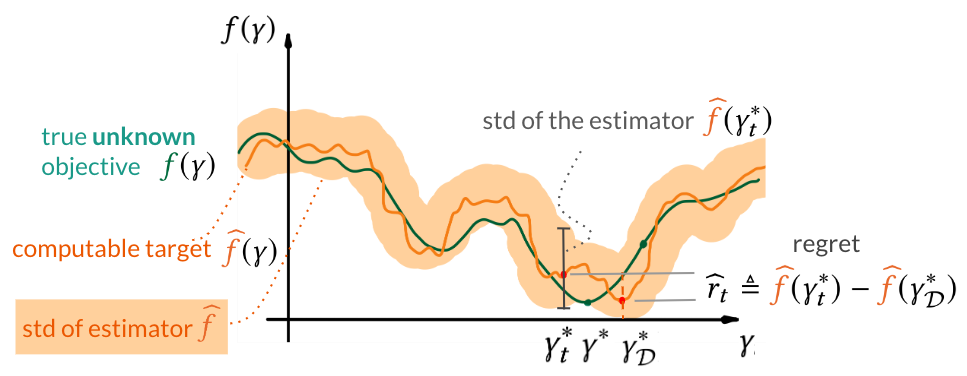
Our termination criterion, then, is that the statistical error exceeds the maximum plausible improvement. This termination condition adapts to different algorithms or datasets and its computation comes with negligible computational cost on top of training the model for some hyperparameter configuration.
Evaluation
We evaluate the stopping criterion over a wide range of HPO and Neural Architecture Search problems, covering the cases where cross-validation is used and when it is not (or can not be). The results show that our method is problem adaptive (in contrast to the baselines). Moreover, it proves an interpretable way to navigate the trade-off between the time use and the accuracy of the resulting model. We encourage you to check the experiments and the main paper for more details.
